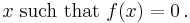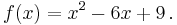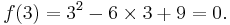Zero of a function
In mathematics, a zero, also sometimes called a root, of a real-, complex- or generally vector-valued function ƒ is a member x of the domain of ƒ such that ƒ(x) vanishes at  , that is,
, that is,
In other words, a "zero" of a function ƒ is a value for x that produces a result of zero ("0"). [1] For example, consider the function ƒ defined by the formula
ƒ has a root at 3 because
If the function maps real numbers to real numbers, its zeros are the x-coordinates of the points where its graph meets the x-axis. An alternative name for such a point (x,0) in this context is an x-intercept.
Finding roots of certain functions, especially polynomials, frequently requires the use of specialised or approximation techniques (for example, Newton's method). The concept of complex numbers was developed to handle the roots of cubic equations with negative discriminants (that is, those leading to expressions involving the square root of negative numbers). Complex numbers also occur as zeros of quadratic equations with negative discriminants.
Every real polynomial of odd degree has at least one real number as a root. Many real polynomials of even degree do not have a real root, but the fundamental theorem of algebra states that every polynomial of degree n has n complex roots, counted with their multiplicities. The non-real roots of polynomials with real coefficients come in conjugate pairs. Vieta's formulas relate the coefficients of a polynomial to sums and products of its roots.
The Riemann hypothesis, one of the most important unsolved problems in mathematics, concerns the location of the zeros of the Riemann zeta function.
See also
References
- ^ Weisstein, Eric W., "Root" from MathWorld.